오늘은 분할 정복을 사용하여 정렬하는 Merge Sort에 대해 알아보겠습니다
Merge Sort는 말 그대로 합치는 정렬입니다
각 부분을 합치는 과정 중에서 해당 값을 비교하여 작은 수와 큰 수를 정렬하는 방법입니다
분할 정복 (Divide and Conquer)
주어진 문제의 입력을 분할하여 작은 부분 문제로 만들고 해당 문제를 해결하여 마지막으로는 전체 문제를 해결하는 알고리즘
→ 부분 문제로 나눌 수 없을 때까지 나누어 해결하여 큰 문제를 해결하는 방식
MergeSort의 경우 각 부분을 입력의 1/2로 나누어 총 분할 횟수는 log2n 입니다
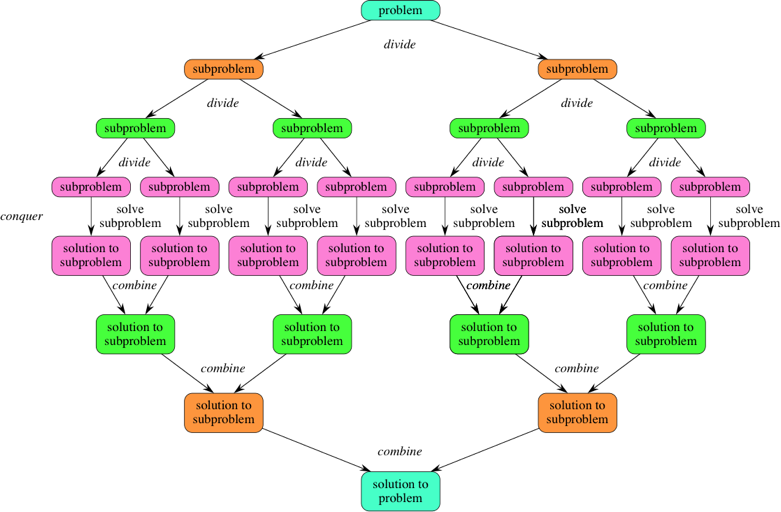
위 그림처럼 자잘한 문제로 나누어 해당 문제를 풀어해결하는 알고리즘
합병정렬 (MergeSort)
병합 정렬이라고도 부르며 해당 정렬 알고리즘은 부분 문제로 나누어서 정렬을 실행하는 분할 정복에 예시
→ 분할 후 합치는 과정도 포함되어 분할 정복을 이해하는 데 큰 도움을 줄 수 있음
분할 정복식 알고리즘 (개념 이해하기) | 병합 정렬 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org

- 정복 → 분할 단계에서 만들어진 두 하위 문제 각각에 있는 하위 배열을 재귀적으로 정렬
- 분할 → p와 r의 중간 q를 찾음→ p와 r을 더해서 2로 나눈 후 내림을 하여 정수로 만듬
- 결합 → 정렬된 두 하위 배열을 하나의 정렬된 하위 배열로 결합
MergeSort 코드 in C++
#include <iostream>
using namespace std;
void merge(int* arr, int first, int mid, int last)
{
int* sorted = new int[last - first + 1];
int i, j, k;
i = first; // First arr idx
j = mid + 1; // Second arr idx
k = 0; // Sorted arr idx
while (i <= mid && j <= last)
{
if (arr[i] <= arr[j]) sorted[k++] = arr[i++];
else sorted[k++] = arr[j++];
}
if (i > mid)
while (j <= last) sorted[k++] = arr[j++];
else
while (i <= mid) sorted[k++] = arr[i++];
for (i = first, k = 0; i <= last; i++, k++) arr[i] = sorted[k];
delete[] sorted;
}
void mergeSort(int* arr, int first, int last)
{
if (first < last)
{
int mid = (first + last) / 2;
mergeSort(arr, first, mid);
mergeSort(arr, mid + 1, last);
merge(arr, first, mid, last);
}
}
int main(void)
{
int arr[] = {38,27,43,3,9,82,10};
mergeSort(arr, 0, 6);
for (auto i : arr) {
cout << i << " ";
}
return 0;
}
MergeSort의 시간 복잡도
- 분할 과정 : O(1)
- 합병과정 : O(m+n) = O(n)
- 각 층별 비교 횟수 : O(n)
- 각 층의 개수 : log2n
층수 * 비교횟수 = O(nlogn)
> MergeSort의 시간 복잡도는 O(nlogn)
분할정복의 한 예시인 MergeSort에 대해 알아보고 해당 알고리즘을 C++로 구현한 후 해당 알고리즘을 분석해보았습니다
'Computer Science > Data Structure & Algorithm' 카테고리의 다른 글
| [알고리즘] Traveling Salesman Problem (55) | 2023.12.02 |
|---|---|
| [알고리즘] 모든 쌍에 대한 최단 경로 구하기 (78) | 2023.10.31 |
| [알고리즘] Kruskal & Prim Algorithm in Python (83) | 2023.10.11 |
| [알고리즘] 벨만-포드 알고리즘 vs 존슨 알고리즘 (21) | 2023.09.21 |
| 존슨 알고리즘 (1) | 2023.08.17 |

